Seitonorika 2020-7,2020年7月10日掲載,ダウンロードPdf
辻村秀信
生徒の理科研究所, 〒623-0342 京都府綾部市金河内町奥地22番地 tsujmr@seitonorika.jp
要旨:科学研究において研究計画の策定や結果から結論を導くときに用いられるさまざまな科学的論理について解説した。科学研究には、因果関係を実証(証明)するための論理、新規仮説の定立のための論理、既知仮説の検証(支持)のための論理、理論分野の論理などがあり、用いられる場面が異なる。内容は以下の通り。①因果関係の証明(実証)のための論理、②因果関係の連鎖を証明するための論理、③帰納法-新規仮説の定立に用いられる論理、④理論研究の論理、⑤検索の論理。
類別:一般記事 分野:生徒理科研究 キーワード:科学的論理、因果関係、帰納法、理論研究
はじめに
科学研究にもちいられる論理には分野の特徴や研究の発展段階を反映して様々なものがあります。これを的確にとらえて正しく利用することは研究を進めるうえで重要です。ここでは、実験・調査計画の策定や、結果から結論を導くときに用いられる科学的論理について説明します。科学的論理には、因果関係の実証(証明)を目的とする論理、新規仮説の定立を目的とする論理、既知仮説の検証(支持)を目的とする論理、理論研究分野の論理、検索のための論理があり、これらの違いを区別して用いる必要があります。
1.因果関係の証明(実証)のための論理
ある実験系に存在する2つの事物(AとB)間の因果関係を実証するための論理を考えます。たとえば「Bの生成にはAの存在が必要である」、あるいは、「AはBの生成にはたらいている」ことを証明(実証)しようとする場合には、次の2種類の実験が必要です(図1)。1つが除去実験、すなわち実験系からAを除去する操作によりBが無くなるあるいは減少することを示す実験、もう一つが付加実験、すなわちAの付加操作によりBが生じるあるいは促進することを示す実験です。この両方が示されてはじめて、「Bの生成にはAが必要である」、あるいは、「AはBの生成にはたらいている」といえます。この2つが示されない場合は因果関係を実証したとは言えません。この論理は実験系における因果関係の解明をめざす科学研究において最も重要なものです。
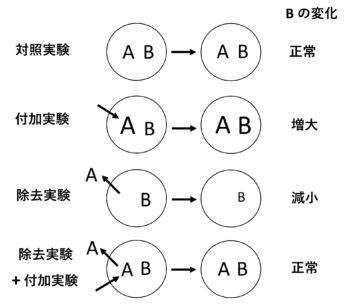
具体例を述べましょう。いま畑でいんげん豆(植物)を栽培しているとします。このいんげん豆の成長の要因を研究します。そこで「植物の成長には肥料(チッソ、リン酸、カリ)が必要である」、あるいは、「肥料は植物の成長にはたらいている」という仮説の真偽を植木鉢栽培を実験系として調べます。まず、畑の土壌を入れた植木鉢に植物を植え、これに肥料を与える実験をします。これが付加実験です(図1)。肥料を与えない場合と比較して肥料を与えた場合に植物の成長が促進されるか否かを調べます。その結果、肥料を与えなくても植物は成長したが、肥料を与えた方がよく成長した場合、「肥料は植物の成長を促進する」ことが分かります。しかし、この実験からは「植物の成長に肥料が必要である」とは言えません。なぜなら、畑の土壌だけを用いた場合でも植物はある程度成長したからです。また、肥料を与えた場合と与えなかった場合でほとんど差なく植物が成長する場合もあるでしょう。この場合の結論は、「肥料は植物の成長を促進しない」となるでしょう。しかし、この結論には「土壌中にすでに肥料成分が十分含まれていたのではないか」という反論が可能です。結局、どちらの場合でも畑の土壌だけで育つ植物の成長が肥料によるものか否かは明らかにできません。
この問題を解決して明確な結論を得るためには、土壌中から肥料成分を除く実験(除去実験)が必要です(図1)。そこで、畑の土壌ではなく、肥料成分をほとんど含まない土壌である「バーミキュライト」または「赤玉土」を入れた植木鉢を用いて植物を育てる実験をします。この実験でもし植物が成長した場合には、「肥料は植物の成長に必要ない」あるいは「肥料がなくても植物は成長する」が結論となります。しかし、もし植物が成長しなかった場合には、「植物の成長には肥料が必要である」あるいは「肥料は植物の成長を促進する」といえそうです。しかしこの場合にも反論が可能であり、畑の土壌には含まれるが「バーミキュライト」や「赤玉土」には含まれない肥料成分以外のもの(たとえば有機物)で植物の成長に必要なものが存在し、「バーミキュライト」や「赤玉土」ではそれが欠けているから植物が成長しないのではないかという疑義です。そこで、必要になるのはバーミキュライトや赤玉土に肥料を加えた土壌をもちいて植物をそだてる実験(除去実験+付加実験)です(図1)。その結果、植物の成長が畑の土壌どおりに回復すれば、「植物の成長には肥料が必要である」、そして、「肥料は植物の成長を促進する」と間違いなくいえます。そして最後に、畑の土壌に実際、肥料成分が含まれているか否かを化学分析で調べます。その結果、適正濃度の肥料成分が検出されれば、畑の土だけで植物を育てた場合の植物の成長がこの肥料成分によるものであることが明らかになります。
以上のように、因果関係の完全な証明には除去実験と付加実験の両方が必要です。しかし、研究課題によっては(現在のところ)片方しか実験処理ができない場合もあります。また、最後の化学分析実験のように仮定した物質を実際に検出できる場合ばかりとは限りません。その時の「結論」は留保付きのものにならざるを得ません。
因果関係には促進の関係だけではなく、抑制の関係もあります。すなわち、AがBを抑制している場合です。この場合の関係もやはり「除去実験」と「付加実験」により研究します。すなわち、抑制がある場合は、Aを除去すればBが促進され、Aを付加すればBが抑制されるはずです。
さらに、因果関係にはより複雑な場合もあります。たとえば、Bの生成にはたらく因子としてA1とA2の2つがあり、A1とA2の両方が存在してはじめてBが生じる場合や、A1 と A2 の両方がなければ B は生じないがA1またはA2のどちらか一方が存在すればBが生じる場合があります。この場合の因果関係の実証もやはり除去実験と付加実験で行いますが、実験のしかたはより複雑になります。
2.因果関係の連鎖を証明するための論理
科学研究では、2因子間の因果関係だけでなく、多因子間の因果関係の連鎖(ネットワーク)を証明するための論理もあります。ここではまず3因子間のネットワークを推論する方法を考えます。
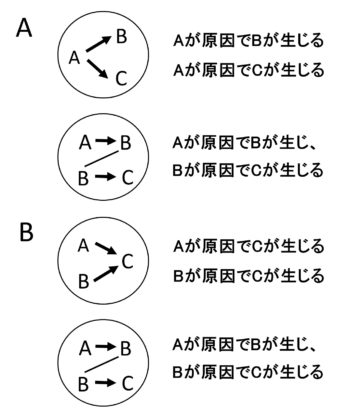
いま、Aという実験処理をするとBとCが生じた。処理をしなければBもCも生じない。この時、片方Bが原因で他方Cが生じるのではないかと推論します。そして、Aが原因でBが生じ、そのBが原因でCが生じるというように因果関係の連鎖(ネットワーク)を推論する(仮説を立てる)わけです。この推論法は、ネットワークを明らかにする時によく用いられます。たしかに「Aが原因でBが生じ、さらにBが原因でCが生じる」が正しいのなら、Aの処理をすると必ずBとCが同時に生じるはずだからです。しかし、この推論が正しいという証拠はありません(図2A)。あくまで仮説としては成り立つということです。
同様に次の推論も可能です。すなわち、Aという実験処理をするとCが生じた。Bという実験処理をするとCが生じた。そこでAの実験処理でBが生じるのではないかと推論を立てます。そして、Aが原因でBが生じ、そのBが原因でCが生じるという因果関係のネットワークを推論する(仮説を立てる)わけです。このばあいも、この推論が正しいという証拠はなく(図2B)、ただ仮説としては成り立つということです。
そこでこうしてつくられた仮説を実験的に証明(実証)するための論理を考えます。一般に、Aが原因でBが生じ、そのBが原因でCが生じることをしっかり証明するためには、すくなくとも以下の4つの実験的証拠が必要です(図2)。①Aの実験処理でBとCが生じる。②Bの実験処理でCが生じる。③Bを除去した上でAの実験処理をしてもCが生じない。⑤Aを除去した上でBの実験処理を行ってもCが生じる。
しかし、実際のネットワークは単純ではありません。因果関係が複雑に絡まっています。実験結果もyes/noのようにすっきりとは出ないことがしばしばあります。そのような時には、さらなる実験的探究が必要になります。
3.帰納法―新規仮説の定立に用いられる論理
一方、2つの事物間の因果関係の存在を推測する(仮説を立てる)ための論理は異なります。よく用いられる論理は帰納法です。たとえば、X条件でBが生じる、Y条件でBが生じる、ところがZ条件ではBが生じない。ここでAについて調べたところ、X条件とY条件ではAが存在したがZ条件ではAが存在しなかった。このようなときに、「AがBの生成にはたらいているのではないか」、あるいは、「Bの生成にはAが必要なのではないか」と推論する(仮説を立てる)論理を帰納法と呼びます。この推論は合理的です。なぜなら、先に上げたX条件、Y条件、Z条件の状態は、「AがBの生成にはたらいている」が正しいときに予想される状態と一致しており、この因果関係の存在を支持している(矛盾がない)からです。したがって、帰納法は因果関係の存在を推測して仮説を立てたり、既知の仮説を実験・調査で検証して支持したりする(矛盾がないことを示す)論理としては有力な方法です。調査研究ではこの論理をもちいた考察がよく行われます。
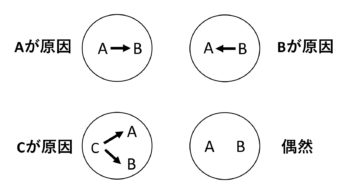
しかしこの論理は、因果関係を証明(実証)する論理ではありません。なぜなら、先の実験結果は、X,Y,Zの3条件では、AとBが一緒に動いていることを示しているだけだからです。この場合のAとBの関係には4通りが考えられます(図3)。①AがBの生成にはたらく場合、②BがAの生成にはたらく場合、③AとBの両方の生成にはたらく別の因子Cが存在し、X条件やY条件ではCが生じ、Z条件ではCが生じない場合、④偶然AとBの動きが一致した場合です。これら4つのうち、④偶然の可能性は実験例数を増やせば減らすことができますが、残りの3つの可能性は減りません。したがって、AとBの動きに一致が見られても両者間にかならずしも因果関係があるとは言えないのです。
結論的には、帰納法は因果関係の存在を推測して新規の仮説を立てたり、既知の仮説を検証して支持したりする(矛盾がないことを示す)のに用いることができるが、因果関係を実証する論理には用いることができません。
4.理論研究の論理
ところが、因果関係の実証ではなく、いくつかの現象をみてその背後に隠れる事物や因果関係を推測する(仮説を立てる)こと自体を、新規の法則(事物や因果関係)を発見するための主要な研究方法とする研究分野があります。除去実験や付加実験で因果関係を証明することが困難な問題を扱う物理や地学、化学、生物の理論研究の分野です。たとえばいま、B1、B2、B3という複数の現象が知られているとします。そこで、B1やB2、B3が生じる原因として、Aの存在と、AがBの生成にはたらくしくみ(因果関係)を説明する新しい理論(多くの場合、数式で表される)とを仮説としてたてます。そして、どのような条件の時AがはたらきB1、B2、B3が生じるのかを理論計算、モデル実験、コンピュータシュミレーションなどを用いて理論的に説明するわけです。
理論研究の分野では理論(仮説)が正しいか否かを実験的に直接証明(実証)することはすぐにはできません。これが困難だから理論(仮説)として発表されるのです。その正しさは、さらに多くの現象(B4、B5)をその理論で説明(検証する、矛盾がないことを示す)したり、別の実験によりAの存在を直接証明したりすることで示されます。すなわち、もし理論(仮説)が正しければ、条件XではB4が生じるはずだと理論的に推論します。そして現実に条件XではB4が生じることを実験的に示すことによってです。あるいは、この理論が正しければ、AはYという性質をしめす事物であると理論的に推論し、実際Yという性質をしめす事物が存在することを実験的に証明することによってです。このような検証実験では、実験結果が理論(仮説)の予想に一致した場合、理論(仮説)を支持する(矛盾のない)新しい事例を見つけたことになり、理論(仮説)の正しさはより強固になります。しかし、理論(仮説)が証明されたことにはなりません。一方、理論にもとづく予想が実験的に否定されれば、その時点でその理論(仮説)はそのままでは正しくないことになります。
このタイプの研究で代表的なものはメンデルの遺伝法則の研究です。グレゴール・ヨハン・メンデルはエンドウを用いた遺伝実験にもとづき仮想的な遺伝子を仮定し、この遺伝子がどのように子孫に伝わり生物の形質を決めるのかを説明する理論(仮説)を提案しました。この理論はその後の多くの実験的検証により一定の修正を受けながらもその正しさが示されてきました。そして今日ではメンデルが仮定した遺伝子が細胞の染色体に存在するDNAの塩基配列であることが実験的に証明され、この法則の正しさは確認されています。
5.検索の論理
研究過程ではその他にさまざまな推論法が用いられます。たとえば、ある条件XでBが存在するとします。ここで、「AがBの生成にはたらく」という因果関係が既知である場合、条件XにはAが存在するのではないかと推測する(仮説を立てる)論理です。この論理は、形式論理学的には「逆は真ならず」で誤った推論です。しかし、BがあるのならAがあるかもしれないと疑うのは自然の推理で、1つのアイディア(仮説)生成法としては成り立ちます。そしてこの仮説生成法は科学研究をすすめるうえでは有用な方法です。もちろん、この推論の正しさは全く保証されないので、その真偽は実験的に証明しなければなりませんが。
ところが実生活の中にはこの論理がより確実性をもって使用される場合があります。検索、すなわち、多くの可能な原因の中から特定のものを選び出すときの論理です。たとえば「Aが原因でB1、B2、B3が生成する」ことが分かっている時、「B1、B2、B3のすべての生成を確認できればAがあるだろう」と推論します。特にB1、B2、B3が偶然にあるいはA以外の理由で、同時に出現する確率が低いことが分かっている場合にこの推論は合理的です。例としては、いくつかの症状にもとづき病気の原因を診断する場合や、いくつかの手がかりをもとに不具合のある機器やシステムの故障個所を特定する場合があります。しかし、このときもAの存在が証明されるものではなく、存在がつよく推測される(可能性が高い)とすべきです。そして、その推測、すなわち診断や故障個所の特定が正しかったか否かは治療(または精密検査)や修理の結果により判断されます。また、生物の種類を同定するための生物検索表もこの論理を用いています。生物のいくつかの特徴を順番にたどっていけば種類名に行き着くように作られています。この場合の真偽は今日では分子生物学的にDNAの塩基配列を調べることにより確認できます。
終わりに
本稿では筆者の生物学分野の研究体験にもとづき因果関係の解明に用いられるさまざまな論理を紹介しました。特に実験系内の2つの事物間の因果関係の証明(実証)のための論理と、因果関係の推測と仮説定立のための論理、既知仮説の検証(支持)のための論理、理論研究の論理の違いを説明しました。生徒理科研究においては、研究分野や研究対象の違いを考慮し、それぞれの研究に適切な論理をもちいることが必要です。
研究には多様な論理が用いられます。その違いは、分野・対象の特徴によります。しかし、それは固定的なものではなく、研究方法の発展によって変化するものです。すなわち、科学が新しい段階に発展したり、新しい方法が開発されたり、取得・利用できるデータの質や量が変化したり、実験方法に対する社会的制約(研究倫理)が変化たりすると、研究に用いられる方法と論理は変化します。したがって、科学研究の論理はこうあるべきだという1つの絶対的規範があるわけではありません。自然に対する認識をより深めたり、自然をより自由に制御したり、社会的制約(研究倫理)によりよく応えたりするのに役立つ方法と論理がそれぞれの時代や社会における科学的論理をつくってきたし、今後もつくっていくのではないかと思います。
この文章は、生徒の理科研究所ホームページ (https://seitonorika.jp)の「論文出版をめざす生徒理科研究法 第3章 研究計画作成法」のために執筆した解説文です。(2020年5月18日)
Ver.2: 2020年7月6日.
